局部变量表和操作数栈实例分析

以圆形的周长公式为例进行分析，下面是Java方法的代码。

public static float circumference(float r) {
    float pi = 3.14f;
    float area = 2 * pi * r;
    return area;
}

上面的方法会被javac编译器编译成如下字节码:

00 ldc #4
02 fstore_1
03 fconst_2
04 fload_1
05 fmul
06 fload_0
07 fmul
08 fstore_2
09 fload_2
10 return

下面分析这段字节码的执行。

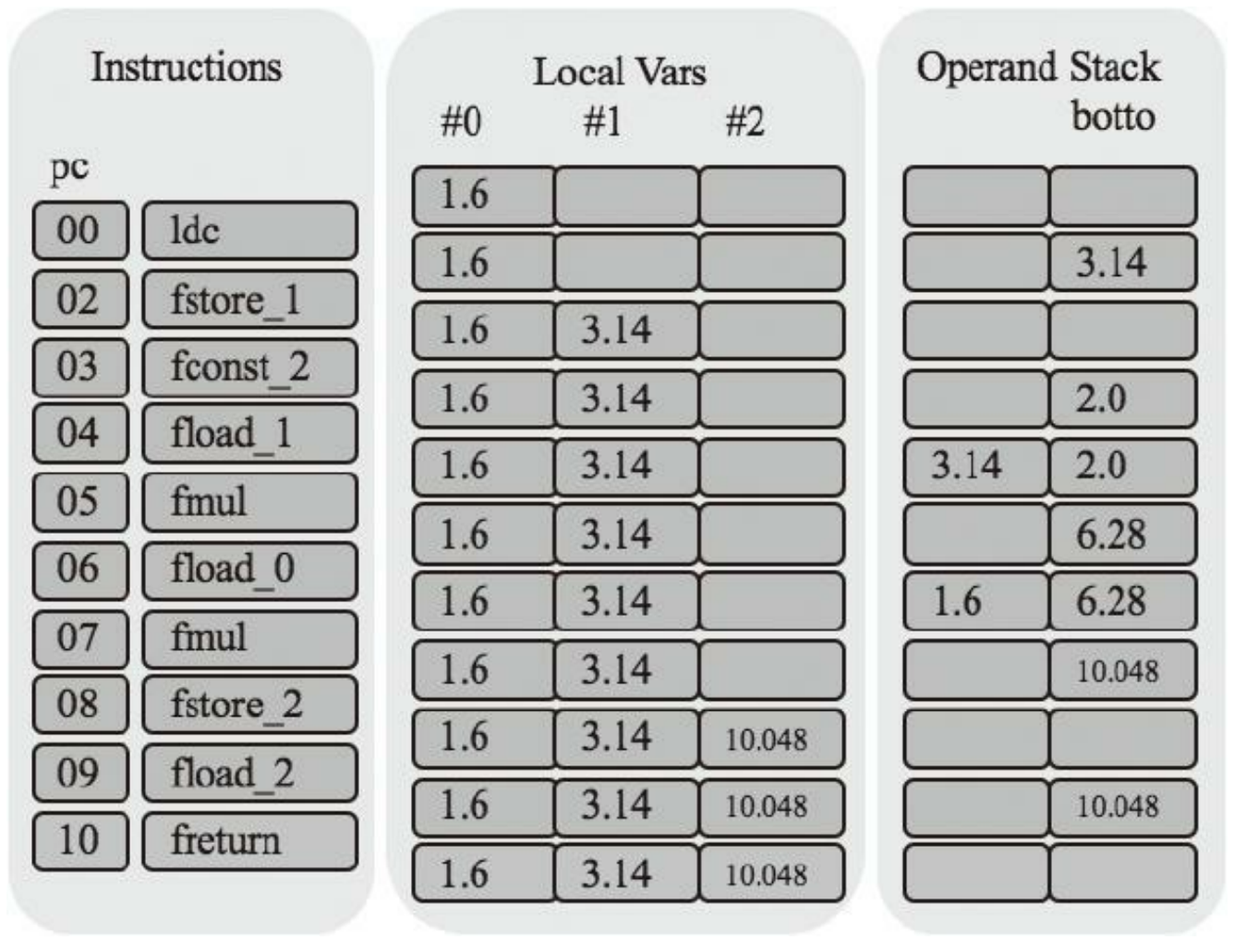
circumference（）方法的局部变量表大小是3，操作数栈深度是2。 假设调用方法时，传递给它的参数 是1.6f，方法开始执行前，帧的状态如图4-3所示。

第一条指令是ldc，它把3.14f推入栈顶

上面是局部变量表和操作数栈过去的状态，最下面是当前状态。

接着是fstore_1指令，它把栈顶的3.14f弹出，放到#1号局部变量中

fconst_2指令把2.0f推到栈顶

fload_1指令把#1号局部变量推入栈顶

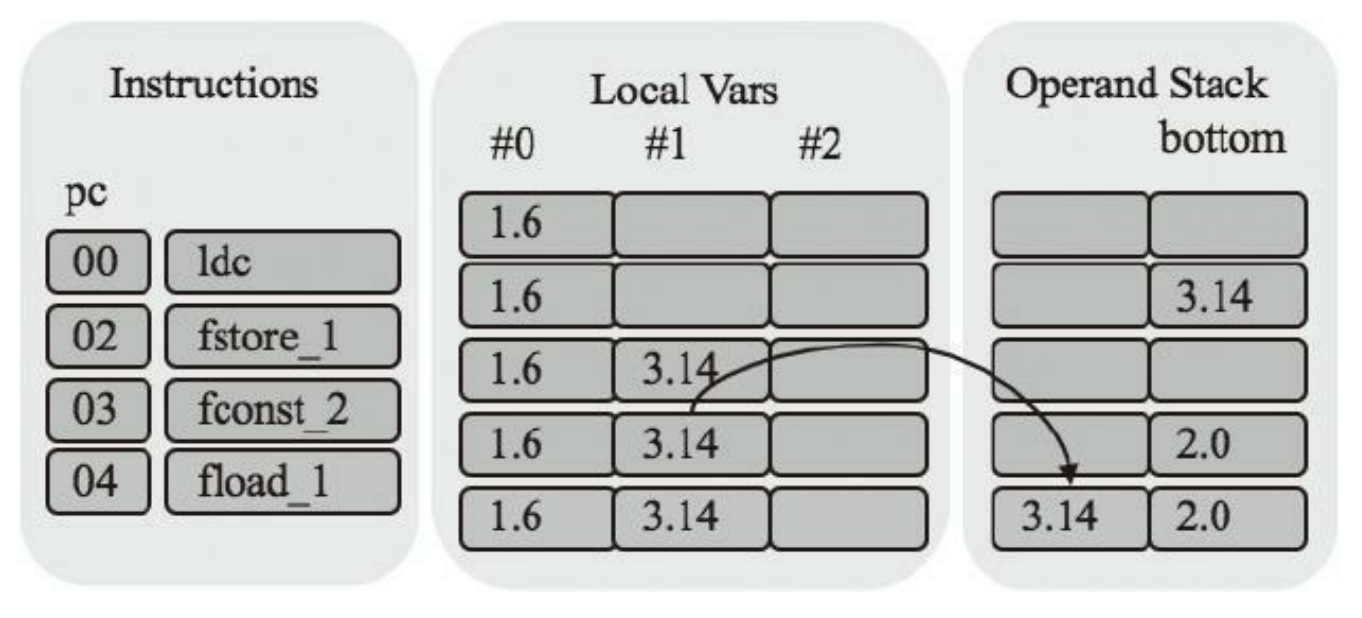
fmul指令执行浮点数乘法。它把栈顶的两个浮点数弹出，相乘，然后把结果推入栈顶

fload_0指令把#0号局部变量推入栈顶

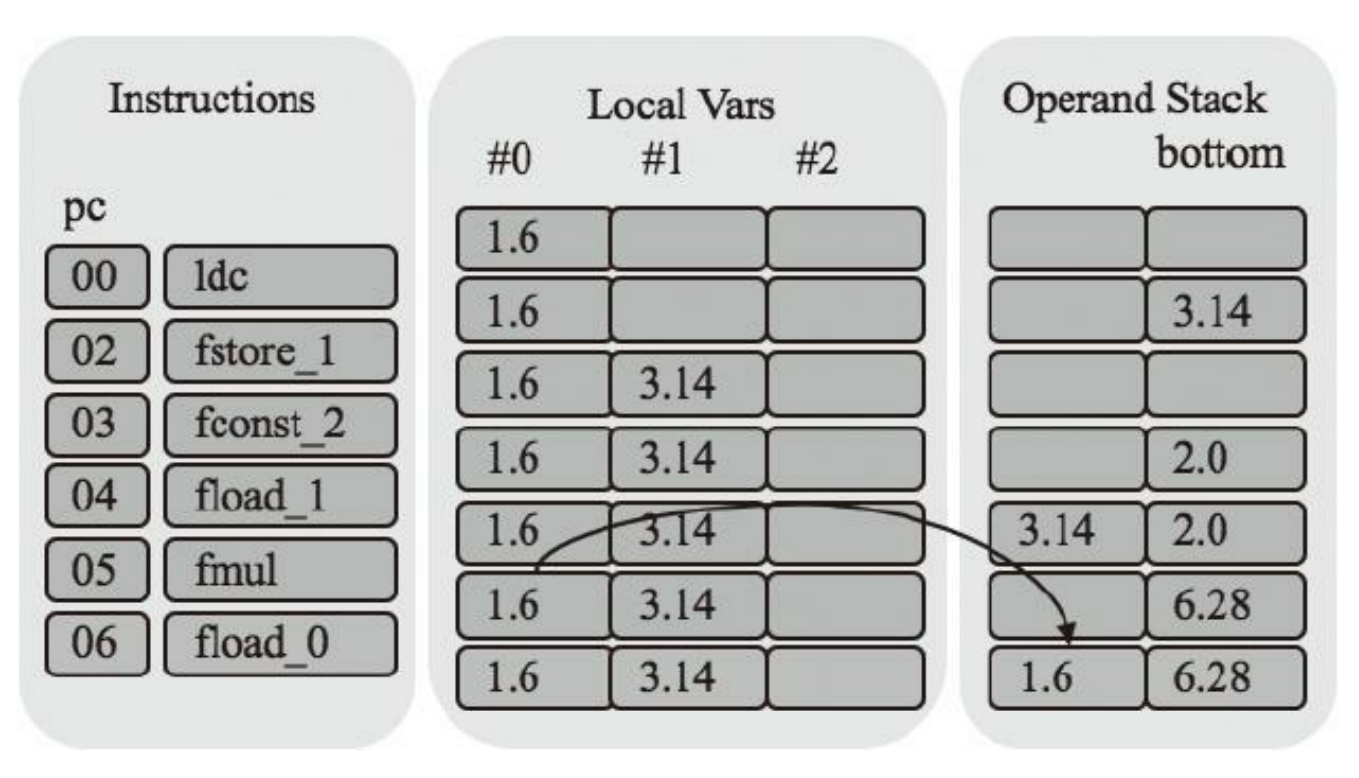
fmul继续乘法计算

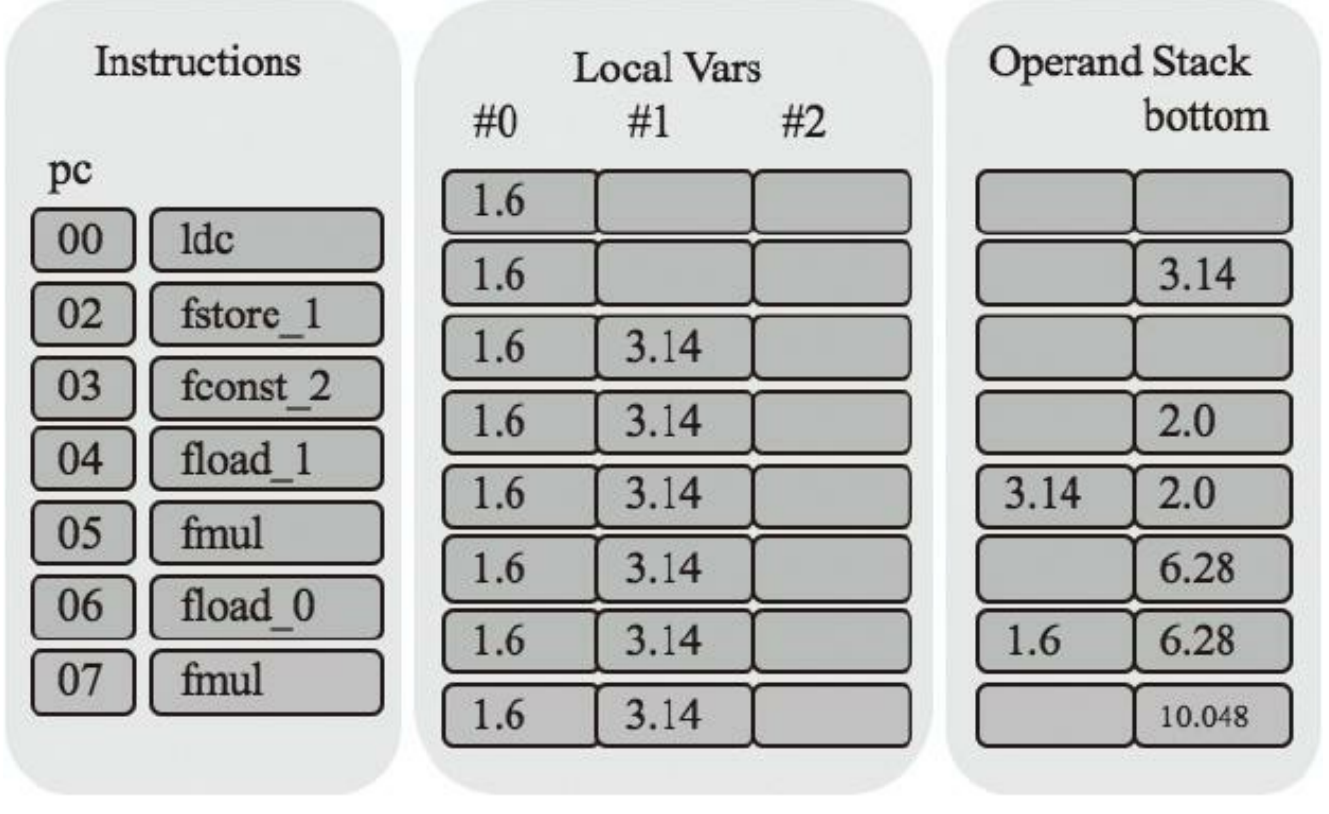
fstore_2指令把操作数栈顶的float值弹出，放入#2号局部变量表

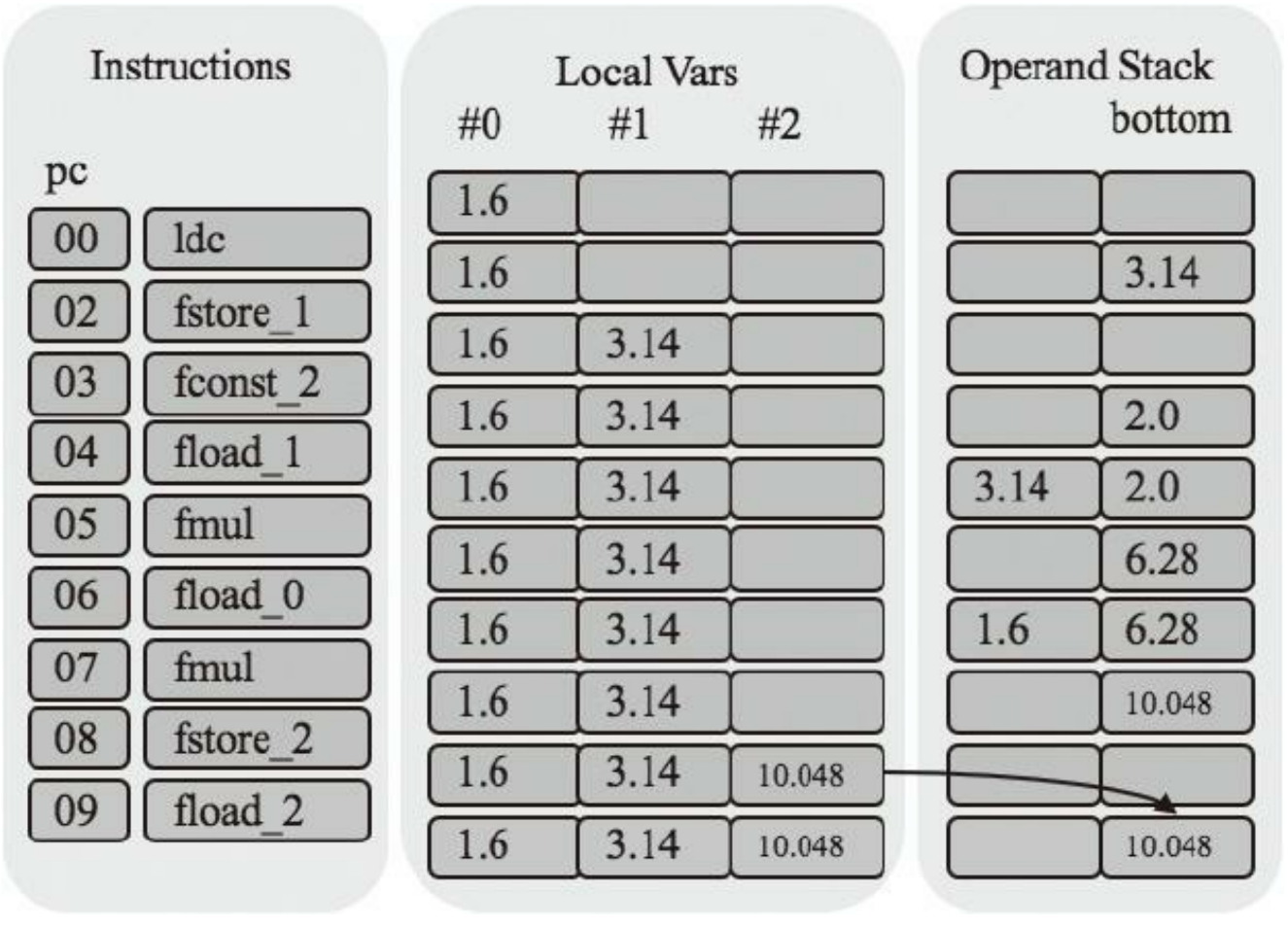
最后freturn指令把操作数栈顶的float变量弹出，返回给方法调 用者